“Llamo a mi esposa: Gala, Galuchka, Gradiva (porque ha sido mi Gradiva); Oliva, por el óvalo de su rostro y el color de su piel; Oliveta, diminutivo catalán de oliva o aceituna; y sus delirantes derivados: Oliueta, Oriueta, Buribeta, Buriueteta, Suliueta, Solibubuleta, Oliburibuleta, Ciueta, Liueta. También la llamo Lionette, porque ruge cuando se enoja, como el león de la Metro-Goldwyn-Mayer; Ardilla, Tapir, Pequeño Negus porque se parece a un animado animalito selvático; Abeja, porque descubre y me trae todas las esencias que se convierten en la miel de mi pensamiento en la atareada colmena de mi cerebro. Me trajo el raro libro de magia que debía nutrir mi magia, el documento histórico que probaba irrefutablemente mi tesis cuando estaba en proceso de elaboración, la imagen paranoica que mi subconsciente deseaba, la fotografía de una pintura desconocida destinada a revelar un nuevo enigma estético, el consejo que iba a salvar del romanticismo una de mis imágenes demasiado subjetivas. También llamo a Gala Noisette Poilue-Avellana Vellosa (a causa del finísimo vello que cubre la avellana de sus mejillas); y también «campana de piel» (porque lee para mí en voz alta durante las largas sesiones de mi pintura, produciendo un murmullo como de campana de piel, gracias al cual aprendo todas las cosas que, sin ella, no llegaría a saber nunca).”
Esta confesión me la hizo Salvador Dalí hace muchos años. Lo recuerdo sobre todo por sus dos obsesiones: su esposa, Gala, y la ciencia, elementos constantes en su vida que, en el momento en el que los conoció, no los dejó ir y marcaron su arte. Quiero contarles sobre una pintura que mezcla a la perfección esto: Leda Atómica, una pintura que hizo mientras vivía en Nueva York, en 1949.

Imagen 1. Leda atómica (1947)
Desde su juventud, Dalí tuvo una obsesión con las matemáticas, la física, la mecánica cuántica y toda una serie de descubrimientos científicos, y se dedicó a estudiarlos y comprenderlos. Alguna vez también me dijo: “Aunque no sea científico debo confesar que los acontecimientos científicos son los únicos que guían mi imaginación”. Y sí, la ciencia nunca lo dejó, ni él a la ciencia.
Para empezar con un primer ejemplo, se preguntarán ¿por qué “atómica”? La respuesta es relativamente simple: durante la Segunda Guerra Mundial (1939-1945) se desarrolló en Estados Unidos la bomba atómica. El descubrimiento de la partición atómica fue, aunque con consecuencias terribles, sumamente importante en el campo de la física nuclear. Esto, en su pintura de Leda, Dalí lo tradujo como una serie de elementos fragmentados y en suspensión. ¿Ya vieron que entre ninguno de los elementos que componen la imagen hay contacto? Todo está flotando y entre esos objetos hay algunos referentes matemáticos como la escuadra y la regla.

Imagen 2. Detalle de los objetos en levitación de la zona inferior
La influencia de la ciencia en este cuadro se puede ver desde varios ángulos, pero ahora nos enfocaremos sólo en las matemáticas, y para entender esto debemos irnos muchos años más atrás. En el siglo XV, en Italia, vivió un fraile que dedicó su vida a las matemáticas. Su nombre era Luca Pacioli y estudió algo que seguramente ya han escuchado: la proporción áurea.
Proporción áurea, divina proporción, número divino, razón áurea, phi o φ, son algunos de los nombres que le han dado los hombres a un número muy particular: 1.618033987… Yendo aún más atrás, esta historia empezó alrededor del 400 a. de C. en Grecia, o al menos hasta ahí se ha podido rastrear. Podemos mencionar a Platón (427-347 a.-C) y Euclides (325-265 a.-C) como dos de los personajes más famosos que conocían esta proporción y la estudiaron, aunque el término de proporción áurea o número dorado, surgió formalmente hasta el Renacimiento.
Se define como el número que resulta de la división en dos de una línea, de forma que si dividimos el segmento más grande entre el más pequeño obtendremos el mismo número que si dividimos la línea completa entre el segmento más largo. Esta proporción se suele redondear a 1.618.

=1.6180339…
Imagen 3. Ecuación general de la proporción
Sus aplicaciones iniciaron en el campo de la geometría: la figura más simple en la que se aplica es el triángulo isósceles, ese que tiene dos lados iguales, de ángulos 36º – 72º – 72º. Como vemos en la imagen 4, se puede segmentar y seguir obteniendo la misma relación de ángulos. Si seguimos segmentando cada triángulo en uno más pequeño y unimos algunos puntos por medio de líneas curvas resultará en la construcción de la famosa espiral logarítmica.

Imagen 4. Formación de la espiral áurea a partir de la división del triángulo
La figura mejor conocida es el rectángulo, cuya formación básica se realiza a partir de la lógica de la secuencia de Fibonacci, matemático italiano del siglo XIII quien definió esta sucesión infinita de números. Por definición, los dos primeros componentes de la secuencia de Fibonacci son el 0 y el 1, y cada número subsecuente es calculado a partir de la suma de los dos números que le preceden.
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
21 + 34 = 55
34 + 55 = 89
55 + 89 = 144
89 + 144 = 233
La relación entre dicha secuencia y phi es que si dividimos el número mayor de la suma entre el menor, conforme avanzamos en la secuencia, este número resultante se va acercando cada vez más a 1.618, de la siguiente manera:
3 ÷ 2 = 1.5
5 ÷ 3 = 1.66
8 ÷ 5 = 1.6
13 ÷ 8 = 1.625
21 ÷ 13 = 1.6154
34 ÷ 21 = 1.619
55 ÷ 34 = 1.6176
89 ÷ 55 = 1.61818
144 ÷ 89 = 1.617977
233 ÷ 144 = 1.618055
Así, siguiendo los número de la secuencia de Fibonacci, se puede construir un rectángulo cuya relación entre largo y ancho vaya de acuerdo a phi y permita también la construcción de la espiral logarítmica que vimos anteriormente.

Imagen 5. Construcción del triángulo a partir de los valores de Fibonacci
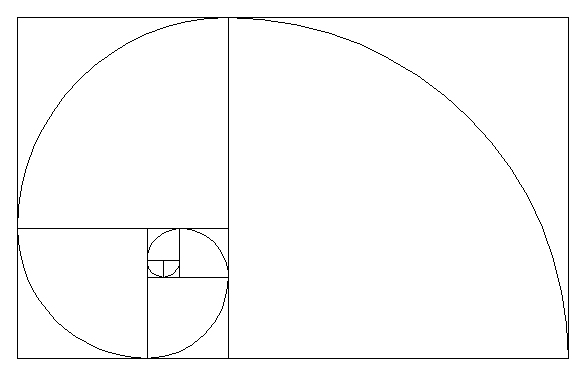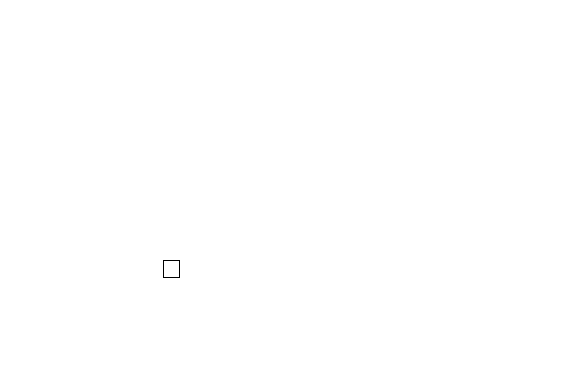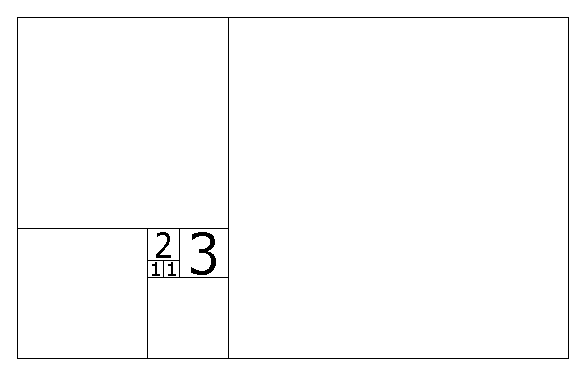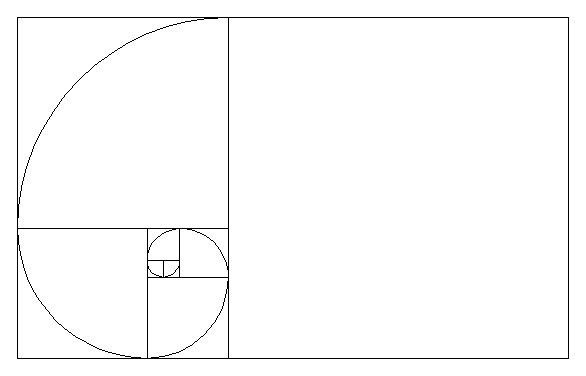
Imagen 6. Creación de la espiral logarítmica
Otra figura muy importante es el pentágono. Al trazar sus diagonales se obtiene el pentagrama pitagórico, el cual en su centro repite el pentagrama externo, invertido. Si observamos bien, este pentagrama está formado por cuatro triángulos isósceles con las mismas características que mencionamos anteriormente. Fue tan importante esta figura desde sus inicios que el símbolo de los pitagóricos era un pentagrama.

Imagen 7. Formación del pentágono; el pentagrama está inserto en líneas punteadas
A este pentágono nos enfocaremos ahora. Entre los documentos que me enseñó alguna vez Salvador Dalí, encontré un boceto de la pintura de Leda:

Imagen 8. Boceto de Leda Atómica
Vean cómo la figura de Gala está inmersa en un gran rigor matemático: ella está dentro del pentágono con el pentagrama trazado al interior, delimitando tanto el espacio que ocupa Gala dentro de la composición, como los elementos que la acompañan. Y aquí es donde se mezclan sus dos grandes amores: Gala era su musa, era perfecta para él y en este cuadro representó y exaltó su perfección y admiración por ella al encuadrarla en la perfección matemática de las figuras de la proporción áurea. ¿No les parece una de las demostraciones de admiración y afecto más bellas?
Y así como Dalí realizó la composición de esta obra (y otras más, como El Sacramento de la Última Cena o Semitaza Gigante Volante con Anexo Inexplicable de Cinco Metros de Longitud), muchos otros artistas han realizado sus obras con relación a la proporción áurea, pues se dice que gracias a ésta logran composiciones más armónicas.
Por siglos se ha creído que las obras de arte más bellas fueron aquellas cuyos creadores usaron la proporción áurea para hacerlas y se ha creído encontrarla en un gran número de pinturas, esculturas, piezas musicales, obras arquitectónicas e, incluso más recientemente, fotografías. Se ha dicho que personajes tan importantes como Da Vinci la usaron en obras maestras como la Mona Lisa o El Hombre de Vitruvio, o que Boticelli la usó para llevar a cabo su tan perfecta obra El Nacimiento de Venus. Sin embargo, hay mucha controversia en torno a aquellas obras.

Imagen 9 La Ultima Cena

Imagen 10 Semitaza Gigante Volante con Anexo Inexplicable de Cinco Metros de Longitud
Finalmente, después de conocer un poco más sobre el número áureo y su relación con la pintura, podemos constatar que la relación entre ciencia y arte es necesaria si hablamos de algunos pintores como Dalí, donde la proporción de las formas reside en las matemáticas.
Autor:
Susana Hoyos es egresada de la Escuela Nacional de Conservación Restauración y Museografía, es tallerista y redactora en La Bombilla IluminArte con Ciencia.
Diseño:
Lina Lucía Romero Salas. Nací en la ciudad de México, desde pequeña tuve inquietud por estudiar artes y fue al terminar esa licenciatura cuando decidí realizar una segunda licenciatura en biología porque siempre me ha llamado la atención la naturaleza. He realizado ilustraciones para distintos laboratorios y actualmente doy un taller de artes plásticas a niños de primaria.
Referencias:
Fundación Dalí (s/f), Biografía de Gala. Recuperado de https://www.salvador-dali.org/es/dali/bio-gala/
Dimensión Dalí (Documental) (2004). Recuperado de https://www.youtube.com/watch?v=23KfoH7dI_c
Bejan, A., (2009), The golden ratio predicted: Vision, cognition and locomotion as a single design in nature. International Journal of Design & Nature and Ecodynamics, vol. 4, nº2, Noviembre 2009, pp. 97-104. Recuperado de https://www.researchgate.net/publication/240977429
Blasco, Fernando (2011), Matemáticas en Dalí. Matematicalia – revista digital de divulgación matemática, 7(4) (diciembre). Recuperado de http://ribf.riken.go.jp/~dang/paintings/fblasco.pdf
Devlin, K, (2012), The Golden ratio & Fibonacci numbers: facts versus fiction. Stanford University. Recuperado de https://www.youtube.com/watch?v=4oyyXC5IzEE
Enzmann, R., (2015), The (ab)surd golden ratio, Ted Talks, TEDxMiamiUniversity. Recuperado de https://www.youtube.com/watch?v=0vVxL60YFJU
Lopez Ferrado, M., (2006), La obsesión de Salvador Dalí por la ciencia. História, Ciências, Saúde – Manguinhos, v. 13 (suplemento), pp. 125-131, octubre.
Risi, M. (s/f), Sucedió en el Siglo XX: la bomba atómica. BBC Mundo. Recuperado de http://www.bbc.co.uk/spanish/seriesigloxx04b.shtml
Livio, M. (2008). The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number, Reino Unido: Crown/Archetype Editions.
Markowsky, G., (1992), Misconceptions about the Golden Ratio. The College of Mathematics Journal, 23(1), pp. 2-19. Recuperado de http://www.jstor.org/stable/2686193
García Cremades, S., (2016), ¿Por qué el número PHI, Φ, es la proporción divina y de oro?. Más Q Parábolas – Blog RTVE. Recuperado de http://blog.rtve.es/masqueparabolas/2016/10/por-qu%C3%A9-el-n%C3%BAmero-phi-%CF%86-es-la-proporci%C3%B3n-divina-y-de-oro.html










